It is easy when sailing to set the GPS system to GOTO waypoint and then steer to match the Bearing (BTW) with the Course over Ground (COG,) or set the autopilot to do so. Provided that Cross Track Error (XTE) is managed, and the course can be made, then the boat will travel directly to the destination. When I do this, I feel that I am lazy, but it seems to work. However, when will this work and when will it not and, how efficient is it in a tideway? There are three cases to consider:
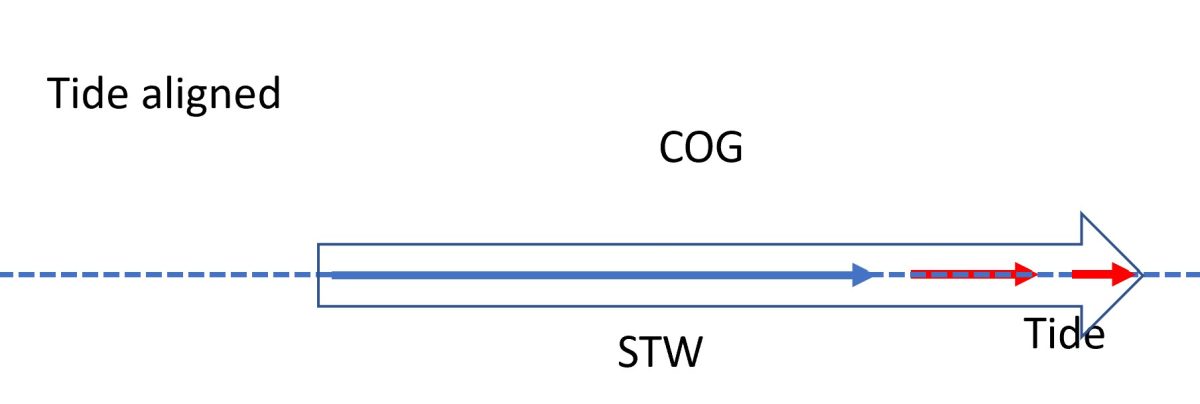
Tidal stream is aligned with the boats heading but varies in velocity. – The boat travels through the water at a Speed Through the Water (STW). If the desired course, and thus heading, aligns with the tidal stream, then the COG and CTS are the same and the only effect is on the Speed over the Ground (SOG) which will be Speed through the Water (STW) plus or minus the tidal stream. the only effect is on the Speed over the Ground (SOG) which will be Speed through the Water (STW) plus or minus the longways Tide. This is the case when the boat is sailing along the coast with the wind free.
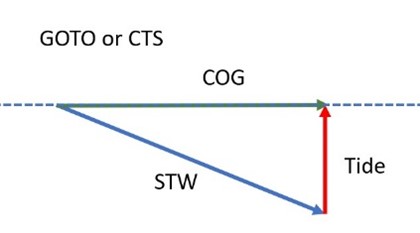
Tidal stream is constant, but not aligned, for the leg concerned. – Where there is an element of sideways tide, it will push the boat off course and affect the course made good (COG) over the ground unless the course steered (CTS) is adjusted (having to beat will complicate matters). Consequently, the CTS and COG will be different as will the STW and SOG. If the GPS is set to GOTO the desired, direct course then, because the water is flowing in a different direction, the boat will travel a longer or shorter course through the water than over the ground and STW will be differ from SOG. However, provided that the boat is kept on the course by managing XTE this method is easy and at least as efficient as a CTS. In this case, the autopilot (or correction of the XTE) performs continuous solution of the tidal triangle.
Tidal stream changes direction and/or velocity for the leg concerned. – The situation is different when the Tide, or an element of it, is at right angles to the desired course. For simplicity, take the case where there is a stream which runs at right angles to the desired course for one hour and then instantly reverses direction for a second hour. Using the GOTO method and staying on course the COG will be as desired, but the boat will have to stem the tidal stream, with the tide running past, first one way and then the other. Because the boat will travel through the two hours of tide, a greater distance is travelled through the water than over the ground. (Skip to the end if you just want to know what to do).
The Speed through Water (for one hour = Distance through water), Tide and COG make the three sides of a right-angled triangle (Pythagoras, remember) for each of the two hours:

1). COG² = STW²-Tide² for one hour, so for both hours: –
2). Total Distance over Ground = COG1+COG2 =√(STW²-Tide²) +√(STW²-(-) Tide²) = 2x√(STW²-Tide²)
If, on the other hand, the two hours of tide are anticipated then, since they are equal and opposite, the CTS will be the same as the desired course. The tide will gradually move the boat ‘s COG away from the desired course over the first hour but then move it back during the second. The navigator will need to check for hazards in the projected ground track. This approach gives a different result since all the STW is used taking the boat to the destination and not stemming the Tide.
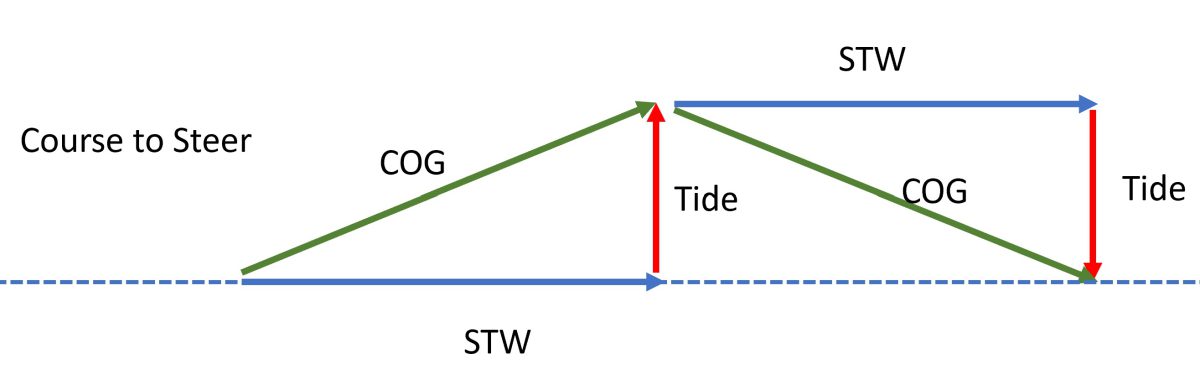
3). Total Distance over Ground = STW1 + STW2 = 2 x STW
As 2) can never be greater than 3) then it should always be as, or more efficient to use the CTS method, provided the calculation is correct (which it will not be).
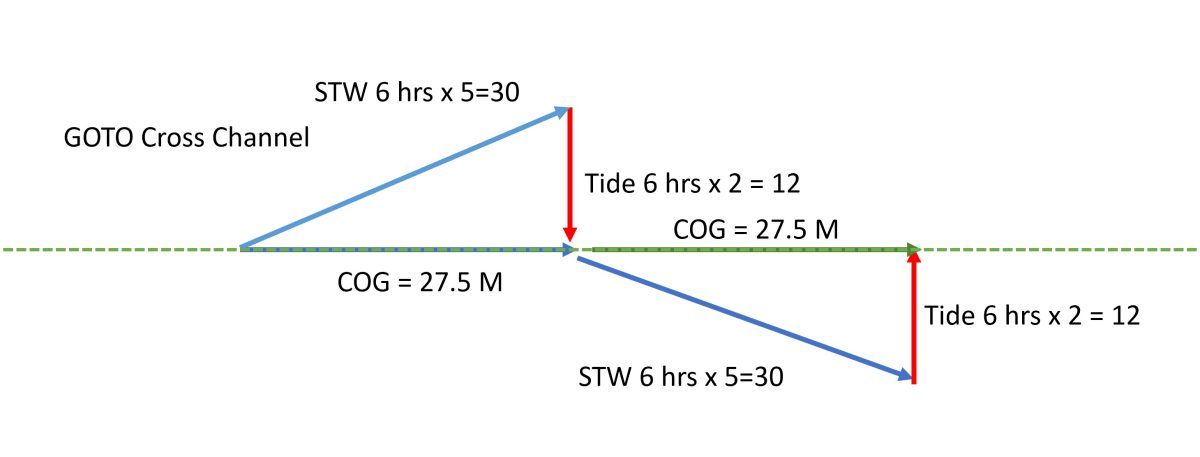
Crossing the English Channel is a good illustration. For example, assume STW=5 and Tide =average 2 for 6 hours East, then 6 West over a complete tide, then distance becomes, for: GOTO method = 2 x √ (25-16) =55 and CTS method = 2 x 30= 60. The GOTO method leaves the boat 5 nM behind and entails another hour of sailing. Obviously, a real case would include several hours of tide at different angles which would make the maths more involved, but the principle holds.
Conclusion
Sailing on the East Coast is generally with or against the tide for short legs so, unless one heads out into the North Sea, there is little chance to experience this issue. For instance, a trip around Roughs Tower is best done with the GPS as it would get the calculations correct through constant iteration rather than calculating a CTS on approximate data. It would be worthwhile, but not make much difference if going to the Spitway from the Naze. However, doing the sums for a CTS is good practice and makes one feel more like a proper sailor and, in any case, one should be using the gizmos as a backup and not the primary means of navigation.