Log Calibration

A yacht’s log records the distance travelled through the water and, from that, derives speed (there are other types of log such as Doppler which work differently). Because the log wheel is subject to the marine environment, such as weed, it ought to be tested often and calibrated to be reliable.

Many sailors are perhaps not much concerned with the accuracy of the log as they rely largely on GPS. However, for classical navigation, whilst an error in the logged boat speed might not be significant, an error in the logged distance travelled does matter, especially on long passages offshore.

Tidal streams will, of course, affect any readings made. A common solution is to perform two runs of known distance and compare them with the averaged logged distances. This method of calculation has an inherent inaccuracy since the effect of the tide is proportional to the time spent in it, consequently, as the boat spends longer on the up-tide leg, it suffers a greater tidal disadvantage than the advantage gained on the down-tide leg.

The following procedure attempts to calibrate the log as accurately as possible and, whilst perhaps over elaborate for most it is an interesting exercise.

Data Required and Errors

The tide cannot be calculated or measured reliably so is an unknown. Managing to perform the calibration when the tidal stream is at a minimum will help alleviate this problem. But, judging slack water is inexact and the rate of change of tidal stream is greatest at this time. On the other hand, the tidal stream is steadiest at full flood or ebb but then its speed is greatest. Whether it is better to have the small but variable tide near slack water or the stronger but constant tide near full flood/ebb remains to be determined.

To eliminate the tide effect, we need the log reading and time for an up-tide and down-tide leg. The trip counter function will give a more precise reading than the main log as it records to 0.01M (18.5m), if a 0.5M course is used then the possible reading error is around 1%. The error in time is negligible since it can be measured to the second by the instrument or a stopwatch.

We also need the distance over the ground which can be measured to better than about 15m over that distance, giving a possible error over a 0.5M course of about 2%. Doubling the course length will halve this but, because it doubles the time spent in the tide this will make it unlikely that the tidal stream will remain constant, unless at full flood or ebb.

So, an error of around 3% is to be expected from measurement errors. If the averaging method is used in a tide then an additional error of, perhaps as much again can be added, more if there is tide.

Procedure – Normal Averaging Method

The normal method goes something like this, often with a focus on STW rather than the distance log. Run up and down tide at a constant speed over a known distance, sum the two log readings and divide them by the total distance over the ground: i.e. R=(Time-up+Time-down)/2*Distance. This ignores the unequal tidal effect on each leg.

Procedure – Rigorous Method

• Note the start time and time of HW.
• The log instrument will already have a correction factor and this will modify the log reading. This factor (let’s call it R) can be reset to 1.0 or applied to the readings to reduce them to the base value.
• Find fairly calm water since waves will have a different effect when the direction is changed.
• Travel a fixed distance over the ground (D), using fixed marks such as buoys, transits or GPS waypoints. Do this in an up-tide and down-tide direction.
• An option for a precise measurement of time and Distance over ground is to record GPS waypoints at the exact start and end of the log recording. The waypoint data will give time and each leg’s start and end waypoints will give distance.
• Keep in line (COG and Compass-True matched) with the tidal stream and run at a constant speed through the water (not SOG), throttle adjustment may be needed to correct for windage.
• Stay in the same part of the channel, a small change can put one in a shallower area with a weaker tide.
• Measure the time up-tide and log-uptide, time down-tide and log down-tide.

Calculation – Rigorous Method

This uses the formula Distance=Speed x Time and some elementary algebra.

• The value of the tidal stream ‘Tide’ or S is unknown but is cancelled out. It can be derived later.
• The sum of log readings up and down tide, would, in theory, equal 2*Distance in still water but the tidal effect is unequal each way and, in any case, the log is in error by the factor ‘R’ (R=1 if it’s correct). So, to get the real log reading we use R*log reading.
• a) For the up-tide leg the distance over ground D = (R*Logged uptide- Tide *Time uptide)* correction R
• b) For the down-tide leg: distance over ground D = (R*Logged downtide +Tide * Time downtide)
• D, the distance over ground is the same both ways so re-arrange a) and b) and equate to remove the unknown Tide.
• The ratio between logged distance and Distance equals the correction factor (R):= (Time downtide*Log uptide+Timeuptide*log downtide)/(Time uptide+Time downtide)*Distance.
• Once R is known the value of the tide, if wanted, can be calculated from a) or b)
• The calculation is obviously tedious to the modern sailor so is best done by a spreadsheet (see below) or app, if there were one.

Log Correction

If the log has recorded a greater distance then R will be <1, if a smaller distance then it will be >1. Once R is known the log instrument can be re-calibrated in the ‘setup’.

The spreadsheet below can be used to do the calculation from knowing times A, B and log readings L_A, L_B and over ground distance, D. Once the correct value of R is known the instruments can be adjusted accordingly.

Verification

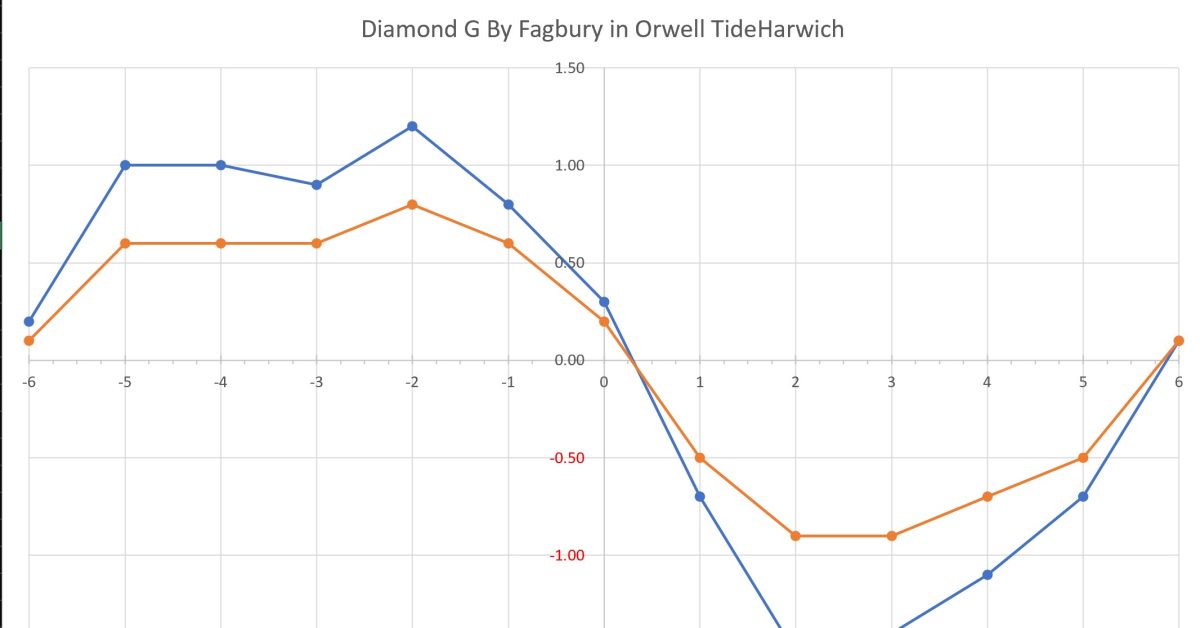
Once the correction factor is known then, if the readings were accurate and the calculation of the R performed correctly, one can calculate what the rate of the tide was on each leg. One would expect the values to be close but not necessarily identical as the speed (S) of the tide is always either increasing or decreasing, especially around the turn: the Diamond data below shows that it can change by 0.75 kts over half an hour which could be two runs.

• Tide S-uptide = (R*Logged uptide -Distance)/Timeuptide
• Tide S-downtide=(Distance-R*Logged downtide)/Timedowntide

This calculation can be performed with either the normal or rigorous method if interested.

Calculator

Use the ‘Calculation’ sheet in the spreadsheet to enter the Log readings, times and Distance and it will output the correction factor.

There is also a ‘Simulator’ sheet which allows assumptions to be made on STW, Distance and Tide to see the results.

Download Spreadsheet

Tidal Diamond

Tidal Diamond G near Fagbury in the Orwell is the only data on the river’s tidal stream. Obviously, these are localised so what follows only applies in that area. It can be seen:

• The rate is zero about 40 minutes after HW.
• The ebb is stronger than the flood.
• The flood is a little longer and steadier than the ebb.
• The rate changes quickly once the ebb starts, from 0 to 0.75kts in half an hour.
• The rate is most constant from HW-5 to HW-2 and HW+2 to HW+3

Notes

In the River Orwell Stratton to Trimley is about 0.4M bearings155/335 about 4 minutes at 6kts. Trimley to No. 1 is about 0.76M bearings 180/000, about 7.5 minutes at 6kts. Bay to No.3 is about 0.83M bearings 110/290. All give a reasonable course in line with the flow and out of the shipping channel.

Some logs have a min/max/average speed function. If this is reset at the beginning of the exercise it can be a useful cross-check.

When determining distances between buoys it is instructive to do this on several different electronic charts as they will give different results.

Setting handheld GPS waypoints at the start and end of each leg gives a precise time and position. The unit needs to be set to record at the maximum precision – once per second if possible.